Computers and computation have been a series of discoveries compared to magic in fantasy worlds with how much we have changed our lives by them, and how its true inner workings continues to elude us. If we divide how we go about computing, it would likely look like this:

• Physical Layer
• Low Level Representation
• Computation Models <- Subject of interest
• Computer Programming
• Systems & Applications

Formal computation models had an optimal computation method for decades that have gone under-utilized: interaction networks. Until recently, there have been few, if any, proper implementations that avoided tremendous overhead, slowing down the graph rewrite to lower than Haskell speeds. A man in Brazil who calls himself Victor Taelin, and his team at Higher Order Co, implemented a virtual machine that limited overhead and allowed for the model’s optimal properties to shine. This intermediate representation is known as Higher Order Virtual Machine or HVM, and has properties that directly expanded my interest in computer science.

Toying around with the tool gave me some extremely valuable insights, and an understanding of why Higher Order Co, and arguably every autonomous AI company, will find their work of particular interest. If you want to understand more about HVM, Interaction Networks, or Interaction Combinators, you can read about it all in a synopsis Victor wrote here.

If you’re wondering why you should find out more: HVM allows for optimal evaluation of lambda terms and trivial memoization and parallelization of all parallelizable and memoizable code. In particular, their clever algorithms related to superpositions, taking advantage of I-Combinator’s graph-based nature to share computation between terms. How this is done, and what it means for enumeration is explored here, with further investigations well under way via implementing it for symbolic planning and other interesting projects.

These are big claims, but I intend to have this blog showcase that it is not merely such.

Let’s dive in shall we?

Superpositions

A quantum superposition is described as the phenomena of which a qubit can simultaneously represent a low and high energy state prior to observation. In bitcode, this is both 0 and 1. Because of this principle, string theorists had questioned if there could exist a dimension where the observed ‘1’ qubit could be ‘0’ in the other, effectively branching the universe. In HVM, this is most certainly true.

Superpositions in HVM are strange to explain without an understanding of Interaction Networks so there will be two. In the appendix will be the more complex answer. Let’s put it simply with an example, inspired by Victor Taelin’s explaination in his blog: \[ \{fn1, fn2\} = x * 10 + 2\] In this scenario, functions \(fn1\) and \(fn2\) both are assigned its followup expression. ‘x’ is undefined and will take an argument within a lambda function. Assume that this program in pseudo-code will run lazily.

\[ \text{Result} = (fn1)(2) + (fn2)(1) \]

The answer to this would most clearly be 43.

\[ \begin{align} \text{Result} = \lambda x.\,(x + 10 \cdot 2)(2) + \lambda x.\,(x + 10 \cdot 2)(1) \\ = (2 + 10 \cdot 2) + (1 + 10 \cdot 2)\\ = 2 + 20 + 1 + 20 \\ = 43 \end{align} \]

Normally, in order for a lambda function to solve this problem, the two cases of the same function must be duplicated, especially in the case of a lazy algorithm, but as you can see, some work is done twice without necessity. We already know what 10 * 2 is, why is this computation repeated?

Superpositions solve this by instead of copying the function, it solves the function once and uses 1 and 2 separately on the partially solved case.

\[ \begin{align} \text{Result} = \lambda x_0.\,(x + 10 \cdot 2)(2) + \lambda x_1.\,(x + 10 \cdot 2) \\ = \{1,2\} + 10 \cdot 2 \, m \\ = \{1,2\} + 20 \\ = 1 + 20 + 2 + 20 \\ = 43 \end{align} \]

This ends up avoiding all duplication of work, instead only duplicating end results for final evaluation. How? It builds the function once, and tosses in the variables twice! By having the functions as a graph instead of a set of lambda terms, the graph can be built and resolved once and re-referenced later. By setting up the original superposition, you are essentially internally labelling a function as the same ‘net’ to be used in the future, much like other memoization work commonplace in computer science, but less fragile and more versatile. (A more technical description will be provided soon, but this works for now.)

I hope you’re skeptical of this claim, so that the demonstrations and graphs in the appendix can prove HVM’s magic, step by step and without any cheats!

The NAND Gate Synthesizer

This program is an automatic circuit builder. It takes a target circuit, tries possible arrangement, tests them all, and returns the first circuit that works exactly the same as the target. There is no room for half answers, although there can be theoretically inefficient ones.

More concretely, a visual:

Here is a circuit of NAND only gates that replicate the function of an AND gate. How do we know this? Look at a truth table:

AND

x	y	output
0	0	0
1	0	0
0	1	0
1	1	1

Both an AND gate and set of NAND gates illustrated above provide this outcome, with the lightbulb at the end only turning on when both x and y are enabled.

A more complex example:

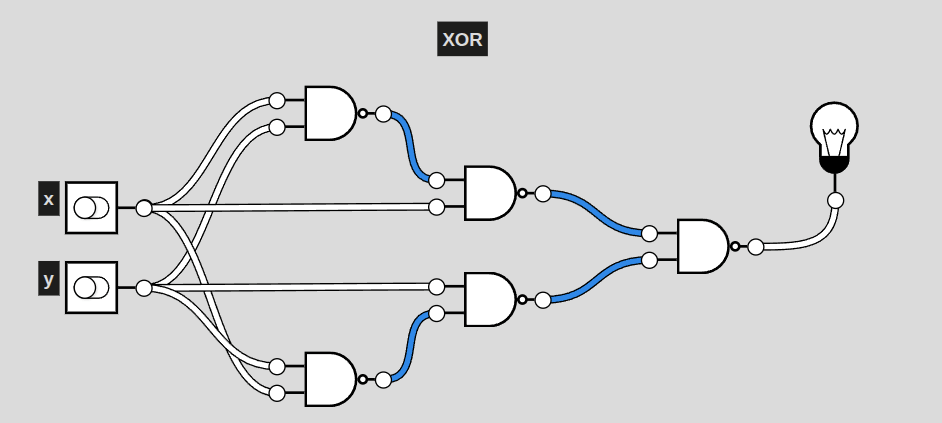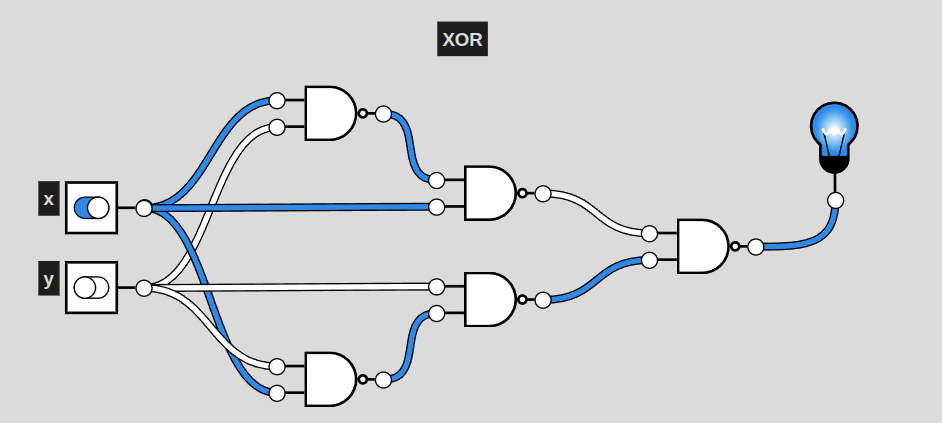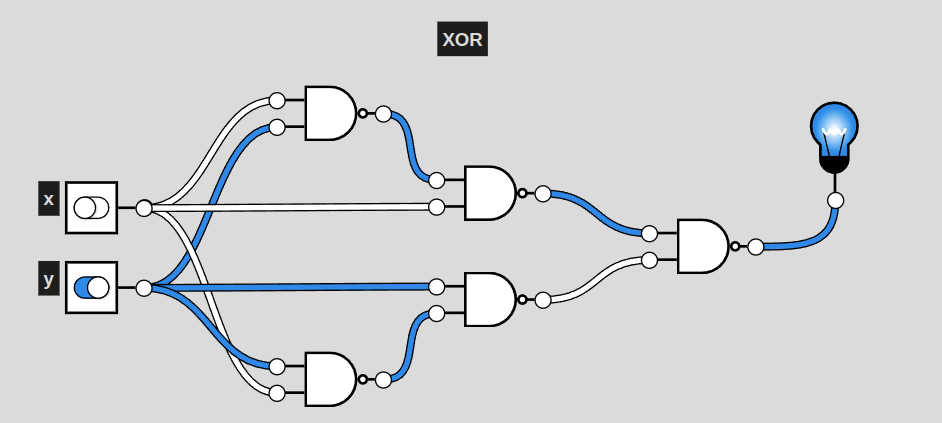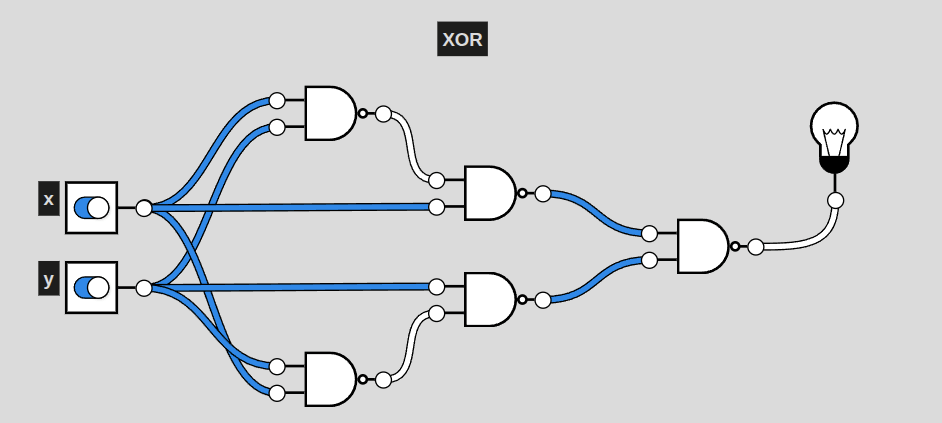
XOR

x	y	output
0	0	0
1	0	1
0	1	1
1	1	0

This particular circuit, a representation of XOR, activates exclusively when only one of the two inputs are active. This is also the shortest a circuit of NAND gates can represent XOR. Even still, it is 3 layers deep (including the first NAND) of NAND gates. AND only had two. More complex circuits will require more and more layers, raising complexity for generating solutions.

In fact, it can be represented with a function:

$$ N(m) = \prod_{i=1}^{m} (i+1)^2 \\ = \Big((m+1)!\Big)^2 $$

Using Stirling’s approximation for factorials,

$$ (m+1)! \sim \sqrt{2\pi (m+1)} \;\left(\frac{m+1}{e}\right)^{\,m+1}, $$

$$ N(m) \sim \left[\sqrt{2\pi (m+1)} \;\left(\frac{m+1}{e}\right)^{\,m+1}\right]^2 = 2\pi (m+1)\;\left(\frac{m+1}{e}\right)^{2(m+1)} $$

Taking the logarithm to highlight asymptotic behavior:

$$ \log N(m) = 2\big((m+1)\log(m+1) - (m+1)\big) + O(\log m) \\ = \Theta(m \log m). $$

Thus the growth rate of the circuit search space is

$$ N(m) = \exp(\Theta(m \log m)) = m^{\Theta(m)} \cdot e^{\Theta(m)}, $$

where \(m = \) number of gates.

Lot’s of math to say that the problem grows super-exponentially as you allow greater and greater depth and increase the number of gates. Coming up with every possibility would be difficult for any sufficiently large circuit. Now, if you’ve done circuit, work you’ll know that this problem is tackled anyway. Tools like Verilog have compilers that navigate this very issue, using tricks and solvers of various kinds to work through this intractable problem. But it turns out that HVM may be suitably equipped to handle them as well, with far less overhead!

Bold claim, so let’s show what’s possible now:

[WIP]